It’s taken a better part of my night, but I’ve finally finished a really difficult homework problem. It feels really satisfying to have it done, especially since it’s in C++, not my usual weapon of choice. I will walk through some of the finer points of the algorithm here, and you can see the whole thing on Github.

Computer science graphs

Graphs are used in computer science to visualize a network of nodes with edges in between them. These nodes can be used to represent users, and the links between them could be the friendships they have. Or, the nodes could represent different lookup servers in a network. Graphs can also be used to represent cities on a map, with the edges being the roads that connect them.

One of the neat problems when given a graph with pre-defined connections and nodes is figuring out how to search through this network. Often, you need to boil down the network into a few necessary connections, that still connect everybody, but remove the overlap of redundant connections. There happen to be two different approaches to this problem, breadth-first search and depth-first search.

In our homework assignment, we had to do a breadth-first search.

Spreading out far and wide

In a breadth-first search, the goal is to start at one node and touch every single node adjacent to that one.

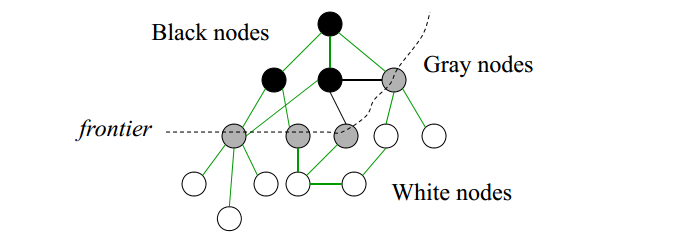
Once you’ve figured out all of the nodes that it is attached to, you go one-by-one through those gray nodes and figure out what’s attached to them. eventually, this will spread across the network and you will have a pretty good idea of what the network really looks like.

Here’s a sample of the code, which is the bulk of the search logic:

// Loop through every node
for (int i = 0; i < total; ++i) {
	// Pop out the first name of the grey nodes, held in the 'q' Queue
	string uName = q->dequeue();

	// Find the node pointer that is associated with that node name
	int uIndex = listIndex(adjList, uName);
	Vertex * u = adjList[uIndex];
	
	// Initialize 'v' to be the first adjacent node
	Vertex * v = u->getNext();

	while(v != NULL) {
		// If the next node is white, turn it to gray, keep track of
		// it's parent and the distance it took to get there, and
		// add it to the queue of gray nodes.
		int vIndex = listIndex(adjList,v->getName());
		if (color[vIndex].compare("white") == 0) {
			color[vIndex] = "gray";
			d[vIndex] = d[uIndex] + 1;
			pi[vIndex] = u;
			q->enqueue(v);
		}
		// Keep iterating through the list of grey nodes
		v = v->getNext();
	}

	// set the initial node 'u' to black
	color[uIndex] = "black";
}

It’s neat that such little code can be used to traverse an entire network of nodes. For those of you who are wondering the efficiency of this algorithm, it’s the same as the depth-first search algorithm, and runs at a speed bounded by the number of edges plus the number of nodes.

In a future blog post, I’d like to implement this in JavaScript and make a comparison. I know a lot of my headaches in C++ came from memory management and static data structures. It would be neat to see how JavaScript handles these problems. See you tomorrow!

---

Tweet

---